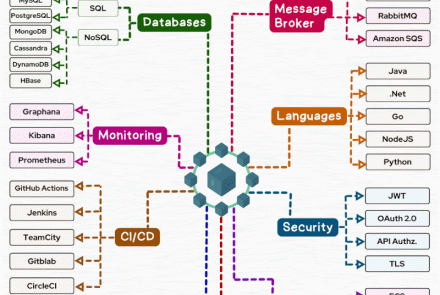
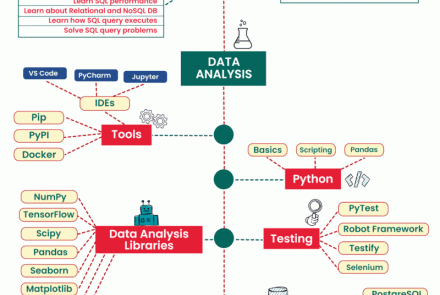
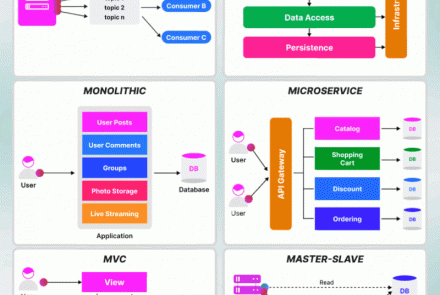
Kỳ thi VMO 2021 đã diễn ra trong 2 ngày 25.12 và 26.12.2020
Bình luận sơ bộ đề VMO 2021
Kỳ thi VMO 2021 đã diễn ra trong 2 ngày 25, 26/12. Sau đây là bình luận sơ bộ của tôi về đề thi năm nay.
Ngày 1 có 4 bài, thuộc các phân môn Giải tích, Đại số, Hình học và Số học.
Bài 1 giải tích có câu a) khá nhẹ nhàng, còn câu b) thì cần đến một đánh giá kỹ hơn một chút. Nói chung là vận dụng tính chất cơ bản: dãy tăng và bị chặn trên thì có giới hạn. Có nhiều cách để đánh chặn na_n, cần tìm ra rồi chứng minh quy nạp là xong.
Bài phương trình hàm có thể xoay xở được, nhưng không phải là bài tầm thường, thậm chí đi sai hướng có thể sẽ không ra và mất nhiều thời gian. Kỹ thuật cơ bản ở bài này vẫn là phép thế.

Bài hình học câu a) không khó, còn câu b) thì có chút thách thức nhưng cũng không phải là quá khó.
Bài số học có câu a) căn bản nhưng câu b là khá phức tạp, sẽ phải rất tập trung và có nhiều thời gian mới xử lý được. Theo tôi, trong bối cảnh ngày thứ nhất có đến 4 bài, trong đó bài 1b), bài phương trình hàm, bài 3b) đều mất thời gian để xử lý thì khó có thí sinh nào có đủ thời gian và sự tập trung để xử lý được bài 4b.
Vì vậy, ở ngày thứ nhất, bạn nào làm được 3.5 bài là rất tốt, 3.0 là tốt và 2-2.5 bài là đạt yêu cầu. Thực tế thì tất cả các ý a) của các bài (tương ứng với việc tìm ra f(1) và xử lý 1 số trường hợp của bài hàm) là "có thể làm được".

Ngày thứ hai có 3 bài, gồm bài 5 (Đại số), Bài 6 (Tổ hợp), Bài 7 (Hình học).
Bài 5 có hai ý, ý đầu liên quan đến nghiệm của đa thức và ý này khá đơn giản, ý sau là một bài bất đẳng thức độc lập, chỉ dùng đến kết quả của câu a) chứ không liên quan gì đến đa thức. Bài 5b này khá thách thức, để giải quyết nó cần biết vận dụng các kỹ thuật xử lý bất đẳng thức nhiều biến: đặt ẩn phụ, đánh giá trung gian. Bài này nếu giải theo tư duy cực trị sẽ có hướng đi tự nhiên hơn.
Bài 6 là một bài tổ hợp khá cơ bản liên quan đến bài toán chia kẹo Euler, những vấn đề đặt ra trong bài toán là tự nhiên và thú vị, không đòi hỏi kiến thức gì cao. Theo góc nhìn này thì bài 5 và bài 6 đều tốt, phù hợp với đề toán olympic.
Bài 7 là bài hình học có ý a) không quá khó nhưng ý b có cấu hình rất rắc rối, phức tạp, kiểu ghép cơ học một ý tưởng khó vào một cấu hình, để giải nó phải dùng đến kiến thức về liên hợp đẳng giác và định lý Desargue, và trước hết phải nhìn ra được cặp điểm liên hợp đẳng giác đó (ví dụ H và O trong cấu hình tam giác bình thường). Đây là một bài rất khó và tôi cho rằng rất khó có thể tìm ra được lời giải trong điều kiện phòng thi.
Theo góc nhìn này tôi cho rằng hai bài 5 và 7 được chế biến theo cách lắp ghép cơ học, một mặt có thể giúp "điều chỉnh" bài toán gốc, nhưng mặt khác làm mất đi vẻ tự nhiên và vẻ đẹp của một bài toán. Ở bài 5, ta sẽ không hiểu được ý nghĩa của việc đánh giá cái tổng đó thì có gì liên quan đến đa thức, còn ở bài 7, việc chồng hình cho chúng ta một cấu hình quá khủng, có đến 14 điểm, hàng loạt đường thẳng và đường tròn chen chân nhau.
Một cách tổng quát tôi cho rằng đề thi VMO năm nay có cấu trúc ổn, vẫn có những bài và ý vừa sức xen cùng những bài và ý khó. Nếu so với năm 2020 thì đề năm nay khó hơn hẳn, không có câu hay ý nào tầm thường, kiếm được điểm nào là xứng đáng điểm đó.
Phân loại các câu và các ý như sau:
- 1) Tương đối dễ: 1a) 3a) 4a) 5a) 6a)
- 2) Trung bình: 1b) 6b), 6c), 7a)
- 3) Khó: 2, 3b)
- 4) Rất khó: 4b) 5b) 7b)
Tương ứng có thể xác định được "tiêu chuẩn" để đạt giải năm nay.
Điểm chuẩn chắc sẽ thấp hơn năm ngoái khá nhiều.